Axial stress, St. Venant’s principle, and Load Path
In the previous article, we discussed potential damage scenarios in thin-walled beams. Now let’s start examining these scenarios one by one. In this article, I will provide some explanations about the importance of the load path concept, which I find extremely significant. More detailed explanations will be provided if requested or as the topic arises over time.
Static Strength
Tension and Compression:
Axial stress (σ) in beams subjected to point tension/compression load (P) can be calculated using the equation σ = P/A, where A is the cross-sectional area of the beam.
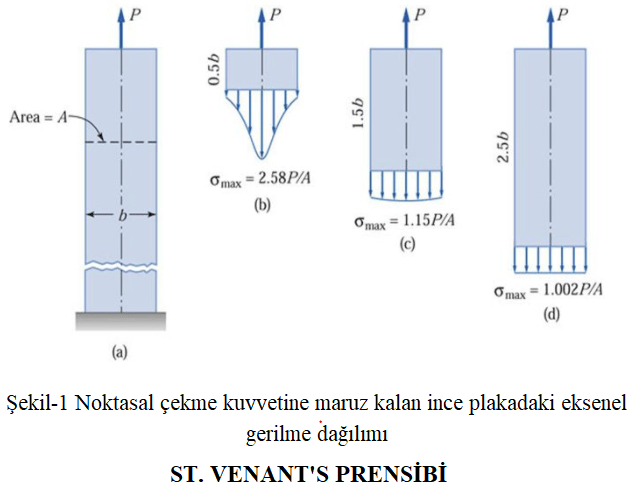
As seen in Figure-1, the location of the cross-section where the stress calculation will be made must be far enough from the point where the singular load is applied for the above equation to be valid. This situation can be overlooked by most engineers and can lead to misinterpretations in finite element models and, therefore, incorrect designs. Therefore, the information provided here should not be seen as unnecessary details.
The main question here should be: Why is the stress distribution in the cross-sections shown in Figure-1(b) and Figure-1(c) not homogeneous? To explain this, we must thoroughly understand the concept of Load Path. In short, load paths are used to describe the flow of a force from the point of application to the reaction point, and the load paths for the loading condition in Figure-1 are given in Figure-2.
Another definition is that load path can be described as the path followed by the load as it is distributed from the point/part of application to the other parts of the system that consist of multiple parts. This is the most important and critical aspect to focus on and be careful about during the design of systems. You can find a few sentences about this in the last paragraph.
I would like to mention that stresses increase where load paths are dense and decrease where they are sparse. In the light of this information, the answer to the question will become apparent.

In more complex loading situations, load paths can be predicted with plenty of mental gymnastics and if necessary, with the help of elasticity theory. For those who find this much theoretical detail overwhelming, practical experience with many examples can be gained through the finite element method and, of course, training their minds in this regard.
In conclusion, it can be said that when designing any system, whether it be an airplane, satellite, or rocket, the fundamental issue is the construction of load paths. Therefore, it is of vital importance. If load paths are not well planned, systems will be unnecessarily heavy and therefore cumbersome. As a result, these designed and manufactured systems will have a short life span, which will lead to products that cannot compete with the world or have low cost/performance ratios.





Leave A Comment